Before start, limit of \(f\) when x-> \(c\) \(NOT f(c) \)

\( f(x) = \frac{x^{2}-1}{x-1} \) is defined everywhere except x=1

\( f(1) \) ?

\( f \) is not defined at \(x=1\)

When x close to 1, \(x \to 1\)

f(x) close to 2, \( f(x) \to 2\)

\( \neq f(1) = 2 \)

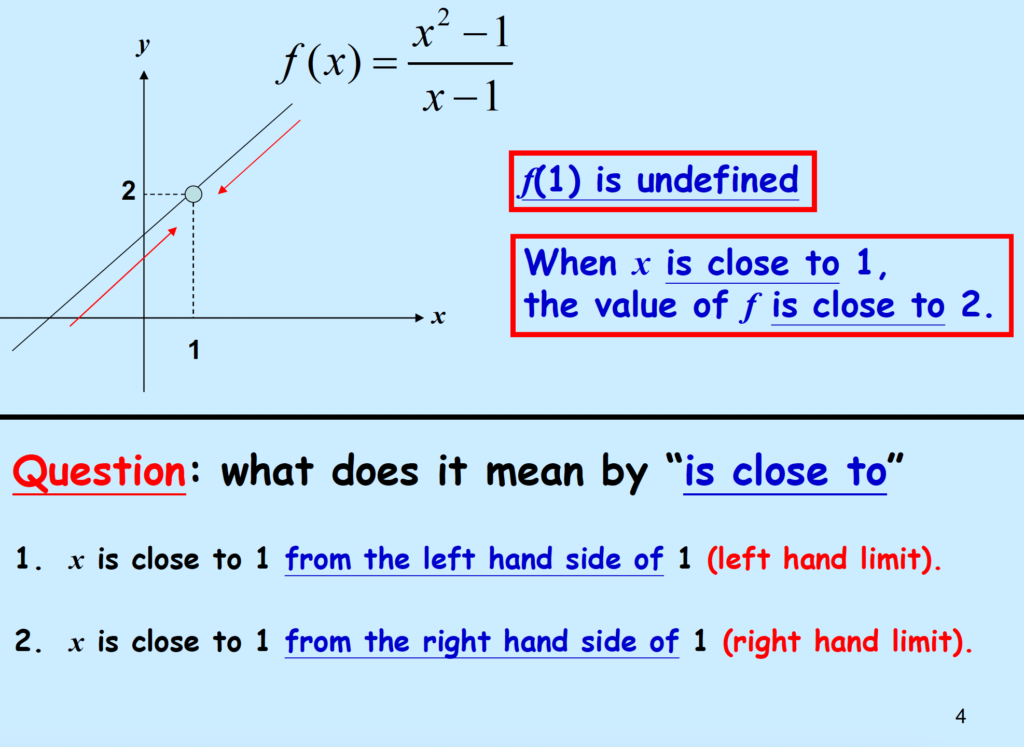
Find limit from both left and right hand.

---

Definition of Limit

Left Limit

\(lim_{x \to c^{-}} f(x) = M\)

Example:

\( lim_{x \to 1^{-}} f(x) = 2 \)

Right Limit

\( lim_{x \to c^{+}} f(x) = N \)

Example: \( lim_{x \to 1^{+}} f(x) =2\)

Limit exists! When M=N

---

Existence of the Limit of a Function

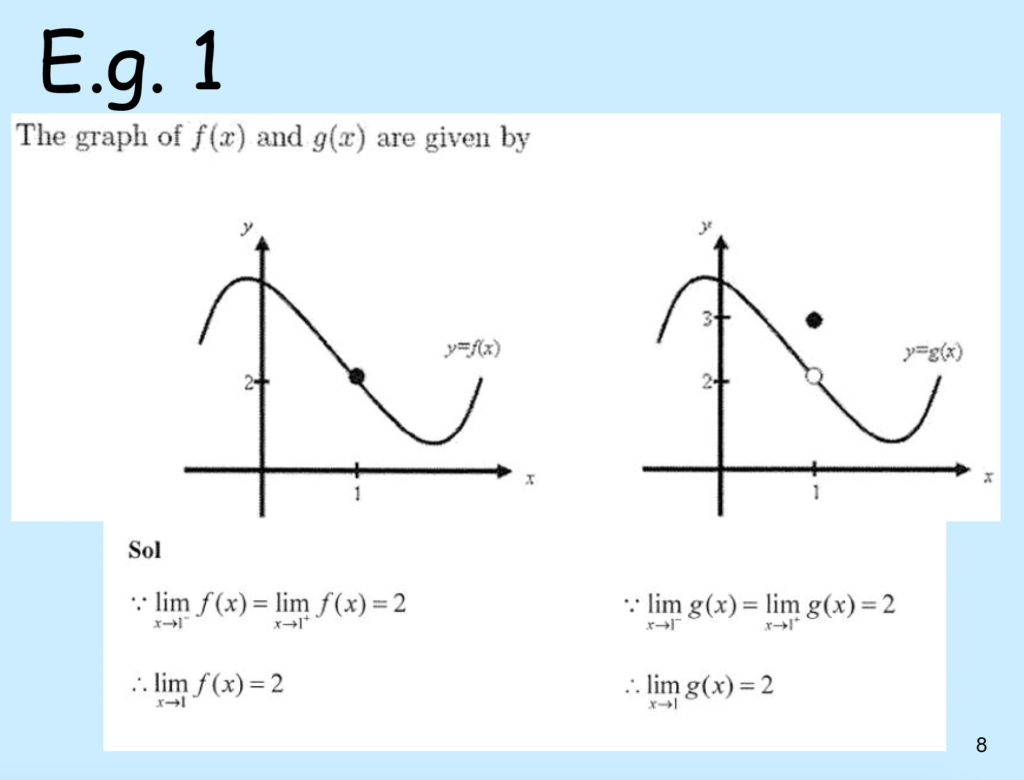
\(f(1)=2\)

Left limit: \( lim_{x \to 1^{-}} f(x) = 2 \)

Right limit: \( lim_{x \to 1^{+}} f(x) = 2 \)

So, \( lim_{x \to 1} f(x) = 2 \)

\(g(1)=3\)

Left limit: \( lim_{x \to 1^{-}} g(x) = 2\)

Right limit: \( lim_{x \to 1^{+}} g(x) = 2 \)

So, \( lim_{x \to 1} g(x) = 2\)

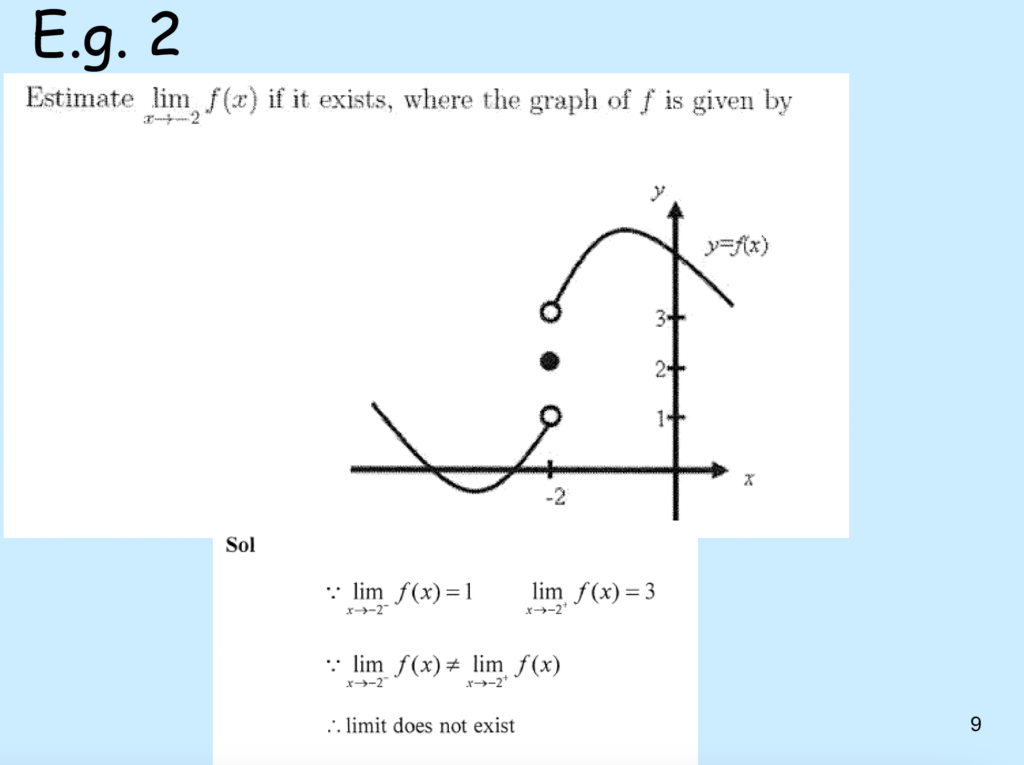
\(y=f(x)\)

\(f(-2) = 2\) , just look at the black dot, there is no explanation for why “2”, this is how it works

Left limit: \( lim_{x \to -2^{-}} f(x) = 1 \)

Right limit: \( lim_{x \to -2^{+}} f(x) = 3\)

\( lim_{x \to -2} f(x) = \)does not exist as left \( lim \neq\) right \(lim\).

ONLY left limit equals to the right limit, limit exist.

Left limit when \( x \to 0^{-} \)

Keep trying values from the left.

\( f(-0.1) \)	\( f(-0.01) \)	\( f(-0.001) \)	\( f(-0.0001) \)
\(= \frac{1}{-0.1} \)	\(= \frac{1}{-0.01} \)	\(= \frac{1}{-0.001} \)	\(= \frac{1}{-0.0001} \)
\(= -10 \)	\(= -100 \)	\(= -1000 \)	\(= -10000 \)

\( \to lim_{x \to 0^{-}} f(x) = -\infty \)

Right limit when \( x \to 0^{+} \)

\( f(0.0001) \)	\( f(0.001) \)	\( f(0.01) \)	\( f(0.1) \)
\(= \frac{1}{0.0001} \)	\(= \frac{1}{0.001} \)	\(= \frac{1}{0.01} \)	\(= \frac{1}{0.1} \)
10000	1000	100	10

\( \to lim_{x \to 0^{+}} f(x) = +\infty \)

\( -\infty \neq +\infty \), therefore, limit does not exist.

Left limit when \( x \to 1^{-}\)

\(x\)	\(0.9\)	\(0.99\)	\(0.999\)	\(0.9999\)
\( f(x)\)	\(1.9\)	\(1.99\)	\(1.999\)	\(1.9999\)

\( \to lim_{x \to 1^{-}} f(x) = 2 \)

Right limit when \( x \to 1^{+}\)

\(x\)	\(1.0001\)	\(1.001\)	\(1.01\)	\(1.1\)
\( f(x)\)	\(2.0001\)	\(2.001\)	\(2.01\)	\(2.1\)

\( \to lim_{x \to 1^{+}} f(x) = 2 \)

\( lim_{x \to 1} f(x) =2 \)

We will not always check left lim and right lim in later, therefore, we have some tricks to check them.

\( lim_{x \to 1} \frac{(3x+2)(x-2)}{5x-2} = f(x) \)

not defined when \( x = \frac{2}{5} \)

Find limit:
\( \frac{[3(1)+2][1-2]}{5(1)-2} \)

\(= -\frac{5}{3} \)

Cannot directly sub 3 into x to check as it will become 0.

\( lim_{x \to 3} \frac{x^{2}-2x-3}{x-3} \)

\( = lim_{x \to 3} \frac{(x-3)(x+1)}{x-3} \)

\( = (3+1) \)

\( = 4 \)

It is nearly impossible to have \( \frac{0}{0} \) in any homework, quiz and exam, this is basically inviting you to factorise.

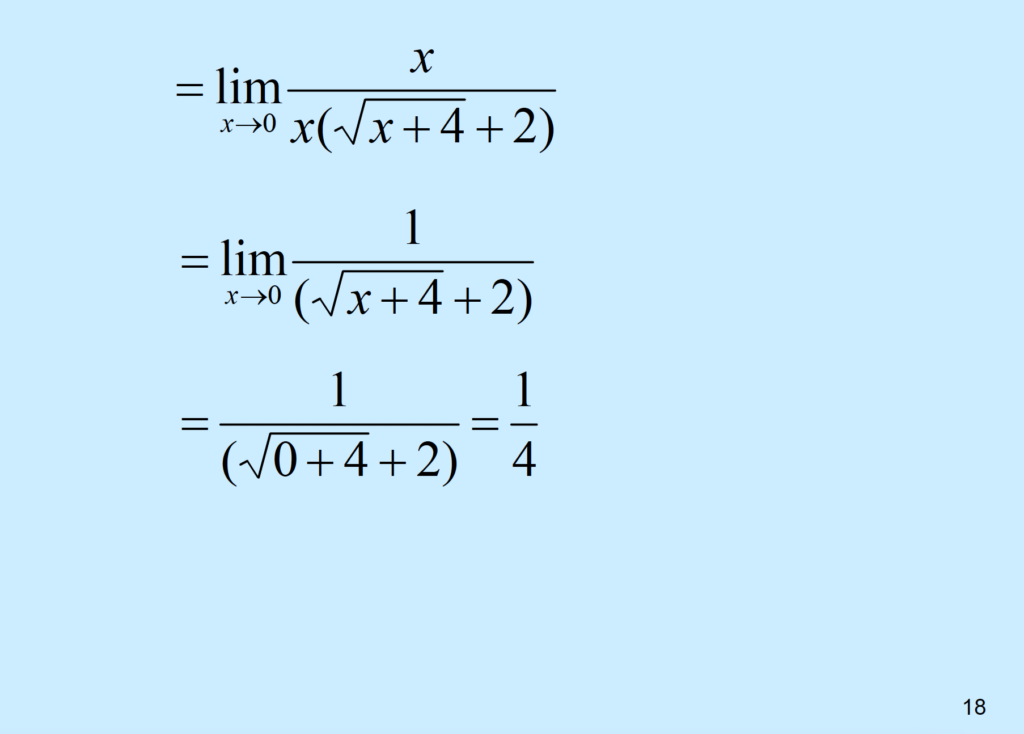
\( lim_{x \to 0} \frac{\sqrt{x+4}-2}{x} \)

\( = lim_{x \to 0} \frac{(\sqrt{x+4}-2)}{x} x \frac{(\sqrt{x+4}+2)}{\sqrt{x+4}+2} \)

\( = lim_{x \to 0} \frac{(x+4)-4}{x(\sqrt{x+4}+2)} \)

\( = lim_{x \to 0} \frac{x}{x(\sqrt{x+4}+2)} \)

\( = lim_{x \to 0} \frac{x}{x(\sqrt{x+4}+2)}\)

\( = lim_{x \to 0} \frac{1}{(\sqrt{x+4}+2)} \)

\( = \frac{1}{(\sqrt{0+4}+2)} = \frac{1}{4}\)

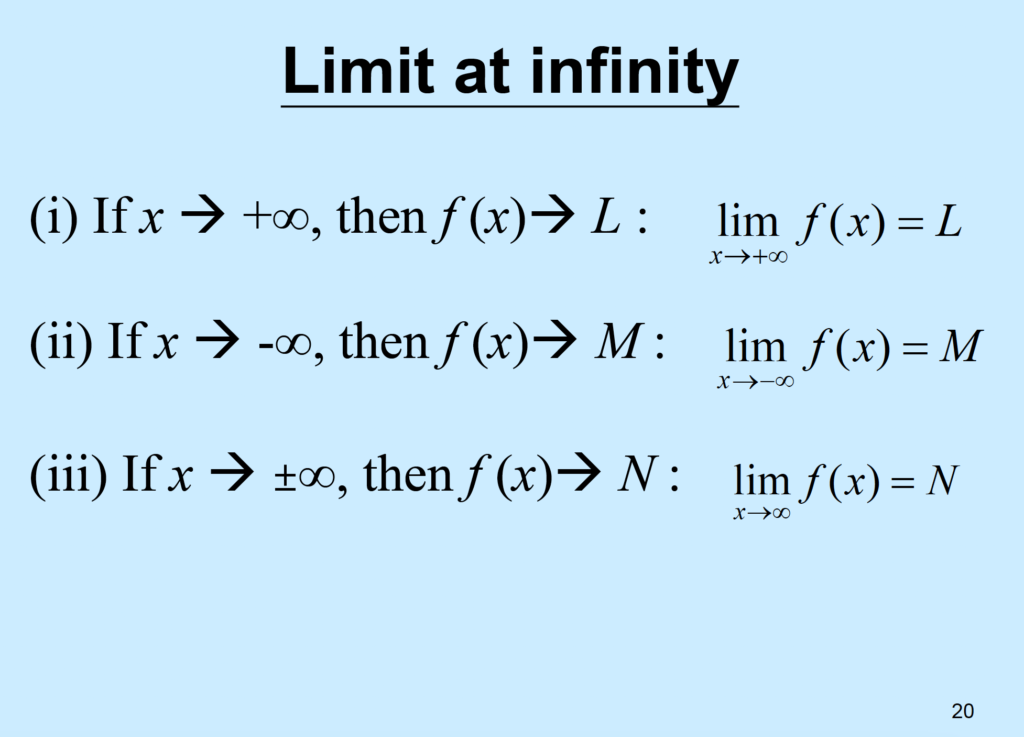
\( lim_{x \to \infty} \frac{1}{x} \) :it will get smaller and smaller, and 0 finally.

\( lim_{x \to \infty} \frac{1}{x} = 0 \)

\( f(x) = \frac{1}{x} \)

\( f(100) = \frac{1}{100} \)

\( f(1000) = \frac{1}{1000} \)

\(g(x)=x \)

\( lim_{x \to \infty} g(x) = +\infty \)

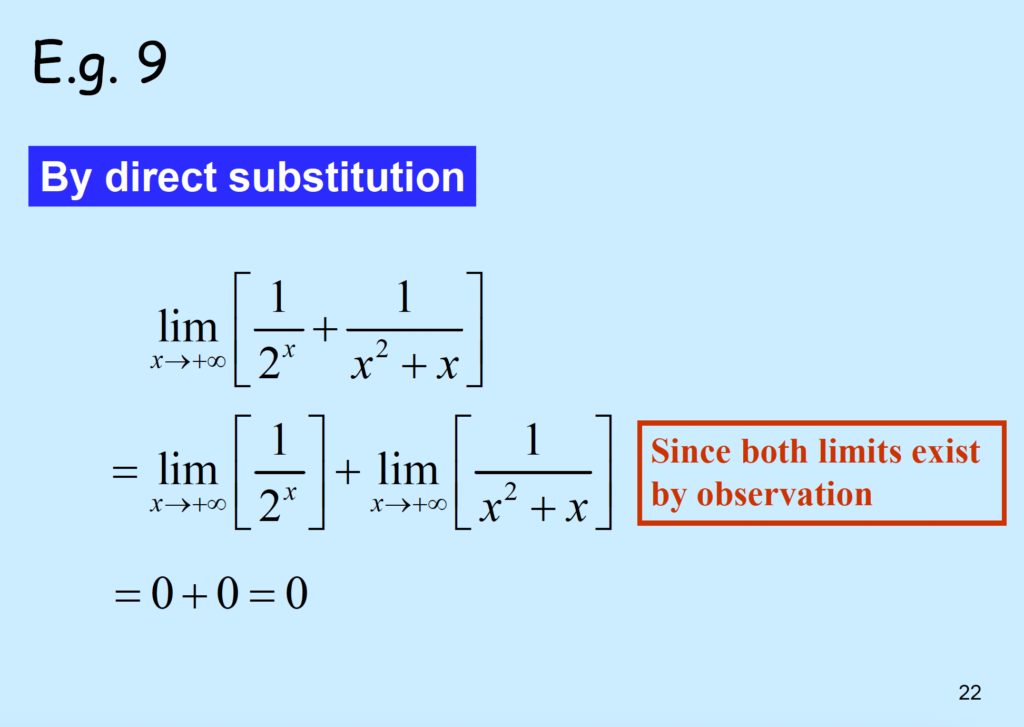
\(lim_{x \to +\infty} [\frac{1}{2^{x}} + \frac{1}{x^{2}+x}] \)

\(lim_{x \to +\infty}[\frac{1}{2^{x}}] + lim_{x \to +\infty}[\frac{1}{x^{2}+x}]\)

\(0+0=0\)

Example:

\( f(10) = \frac{1}{2^{10}} + \frac{1}{10^{2} + 10} \)

\( lim_{x \to \infty} [x^{4} – \pi x^{2}] \)

\( = lim_{x \to \infty} x^{4} – lim_{x \to \infty} \pi x^{2}\)

WRONG!!!

\( ~ lim_{x \to \infty} x^{4} = \infty\)

\( \to \) limit does not exist.

\( lim_{x \to \infty} \frac{2x^{3}+3}{3x^{3}+1} \)

Tips: always the guy with the highest power.

\( = lim_{x \to \infty} (\frac{2x^{3}+x}{3x^{3}+1}) (\frac{\frac{1}{x^{3}}}{\frac{1}{x^{3}}}) \)

— As of 2023-09-19 19:30

___ Start from 2023-09-26 16:50:23

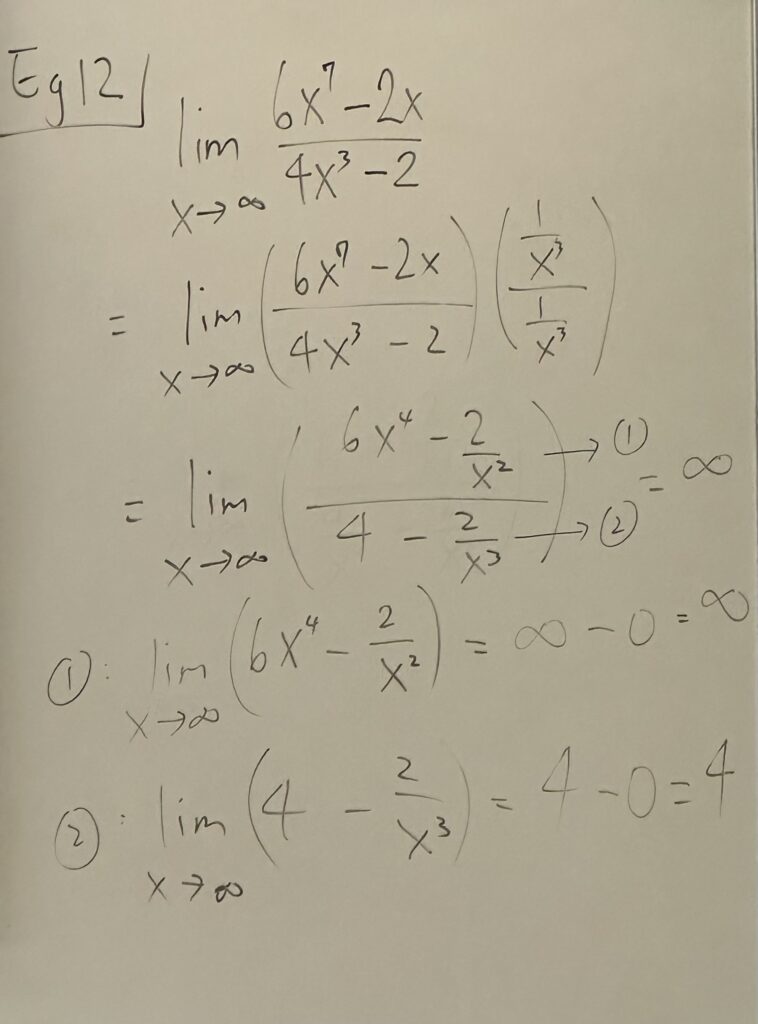
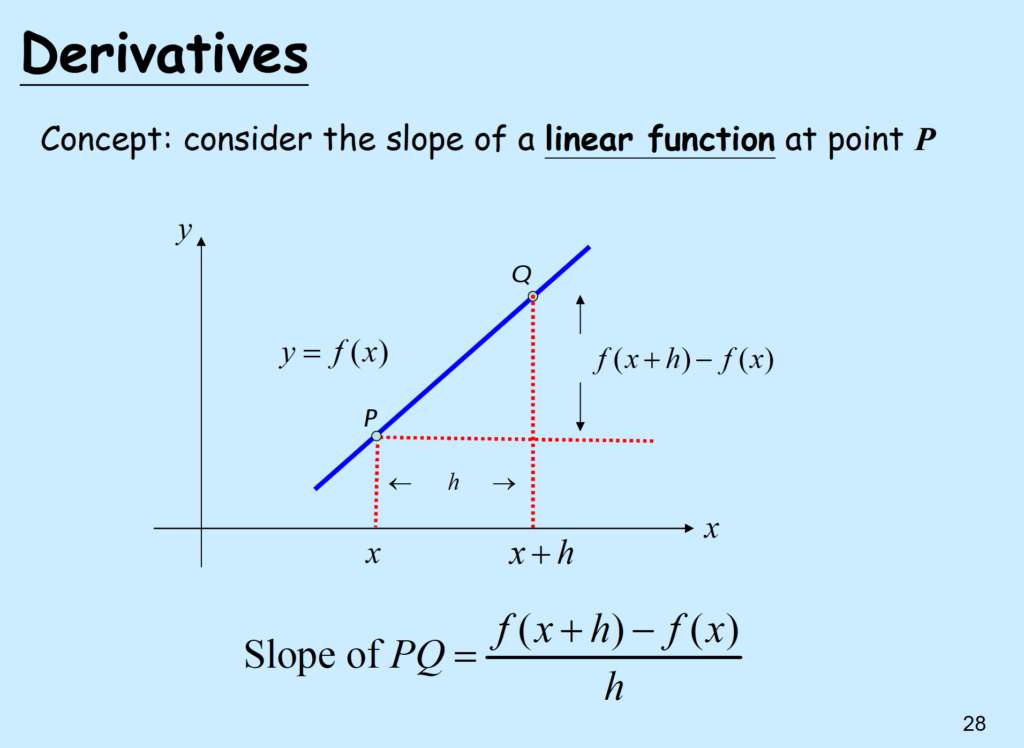
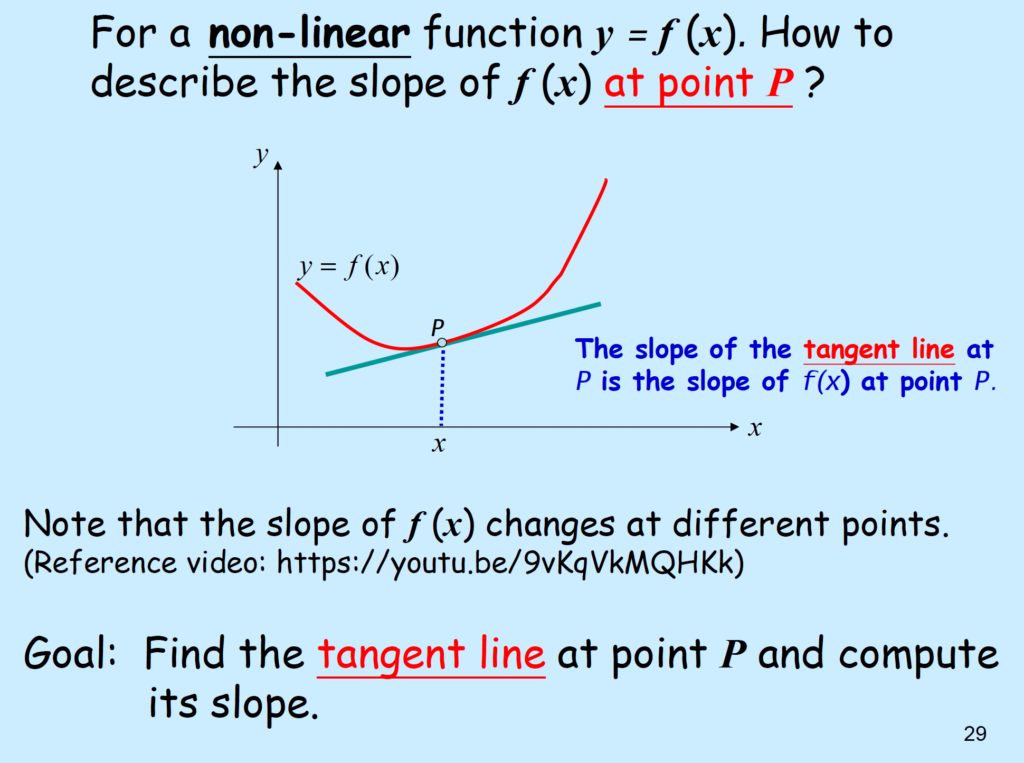
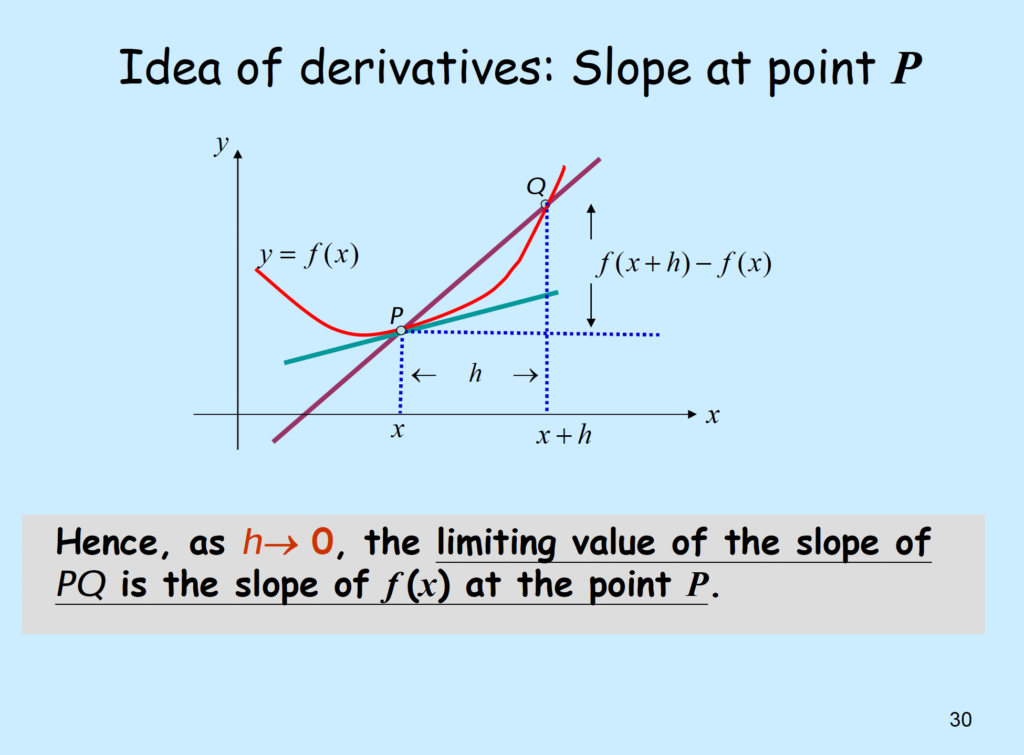
Slope of any function = derivative: \( \frac{df}{dx} = f(x) = y’ \)

2023-10-3 5:07pm

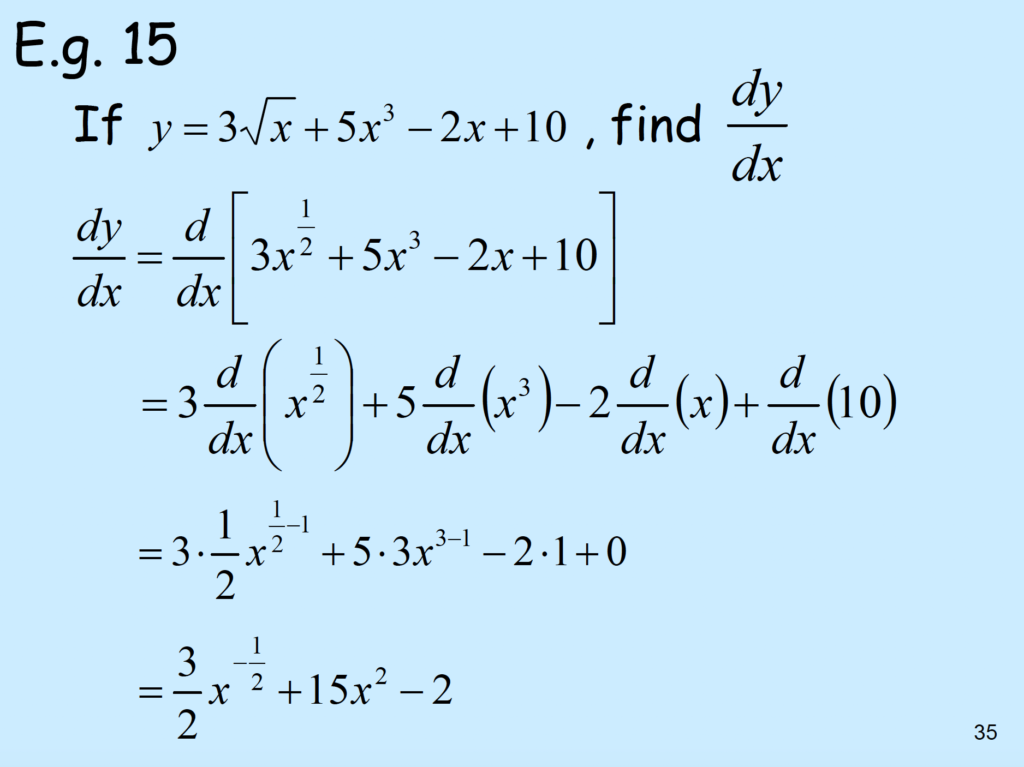
Differentiation Rules:

1. \( \frac{d}{dx}(C) = 0\)
2. \( \frac{d}{dx}(x) = 1\)
3. \( \frac{d}{dx}(x^{n})=nx^{n-1} \)
4. \( \frac{d}{dx}[u(x)+v(x)] = \frac{d}{dx}u(x) + \frac{d}{dx}v(x) \)
5. \( \frac{d}{dx}[Cu(x)] = C \frac{d}{dx}u(x)\), C is constant.

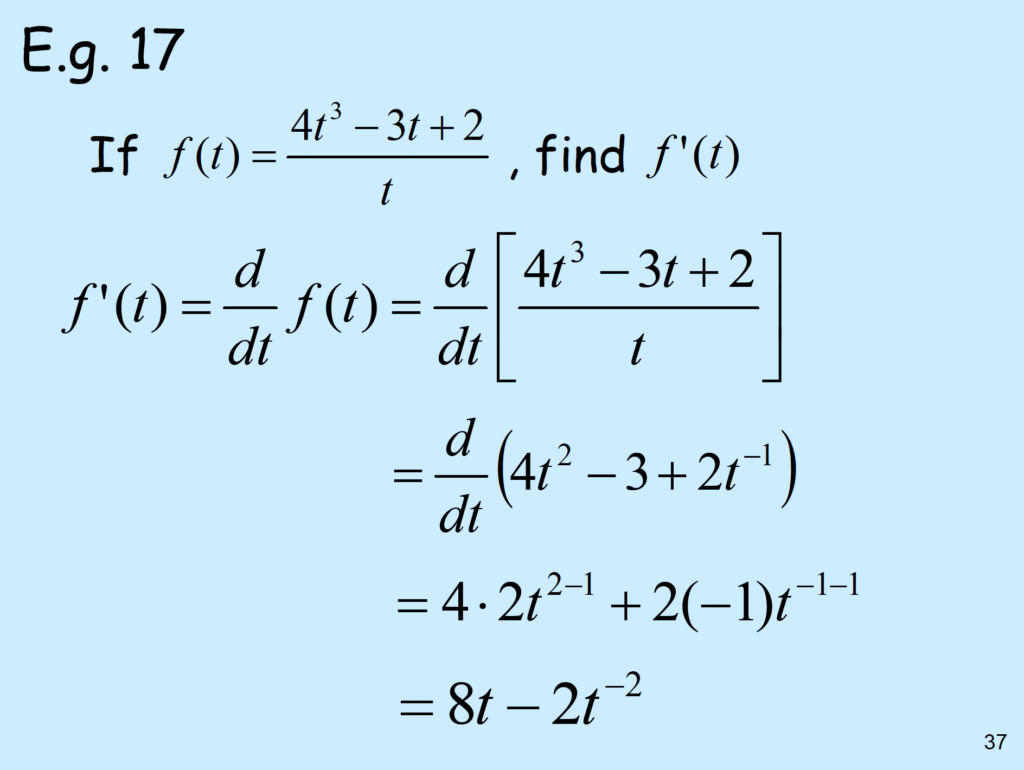
2023-10-3 5:07pm

\( f(u) = u^{3} \), \( u(x) = 2x^{2} + 1\) find \(\frac{df}{du}\), \(\frac{du}{dx}\), \(\frac{df}{dx}\).

\( f'(u) = \frac{df}{du}\) [using DR3] = \( 3u^{3-1} = 3u^{2}\)

\( u'(x) = \frac{du}{dx} = \frac{d}{dx}(2x^{2}+1) = \frac{d}{dx}(2x^{2}) + \frac{d}{dx}(1) = 2\frac{d}{dx}(x^{2}) + \frac{d}{dx}(1) = 2(2x^{2-1}) + 0 = 4x \)

\( f(u(x)) = (2x^{2} + 1)^{3} \)

\( \frac{df}{dx} \) [using DR8] \( = ( \frac{df}{du} ) (\frac{du}{dx}) = (3u^{2}) (4x) = 3(2x^{2} + 1)^{2} \times (4x) = 12x \times (2x^{2} + 1)^{2}\)

\( f(x) = (x^{2} -4x +3)^{1234}, find \frac{df}{dx}.\)
\( u(x) = x^{2} – 4x + 3, f(u) = u^{1234} \to f(u(x)) = (x^{2} -4x+3)^{1234}\)

[DR8] Chain Rule: \( \frac{df}{dx} = (\frac{df}{du} ) \times ( \frac{du}{dx} ) \)

(1) \( \frac{df}{du} = \frac{d}{du}(u^{1234}) [DR3] = 1234 u^{1234-1} = 1234 u^{1233} \)

(2) \( \frac{du}{dx} = \frac{d}{dx}(x^{2} -4x+3)=\frac{d}{dx}(x^{2}) [DR3] -4\frac{d}{dx}(x) + \frac{d}{dx}(3) = 2x -4(1) +0=2x-4\)

\( \to \) [DR8] Chain Rule: \( \frac{df}{dx} = (\frac{df}{du} ) \times ( \frac{du}{dx} ) \)

\( =(1234u^{1233}) \times (2x-4) \), don’t stop, goal: express in terms of x.

\( = 1234(x^{2} -4x+3)^{1233} (2x-4)\)

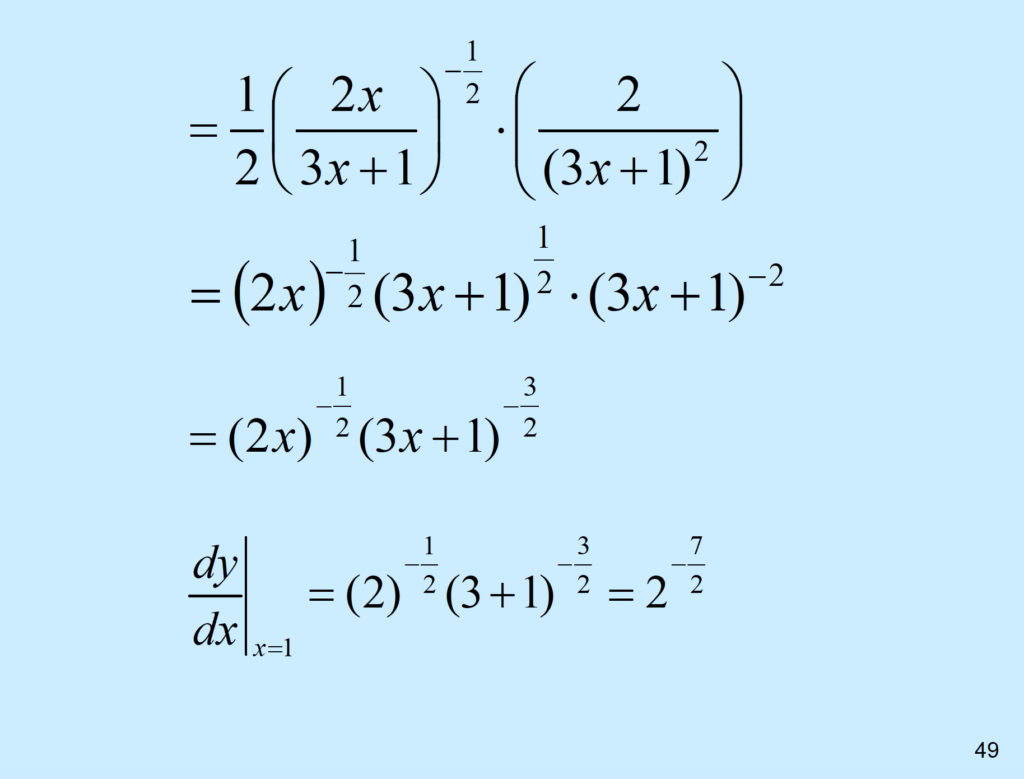
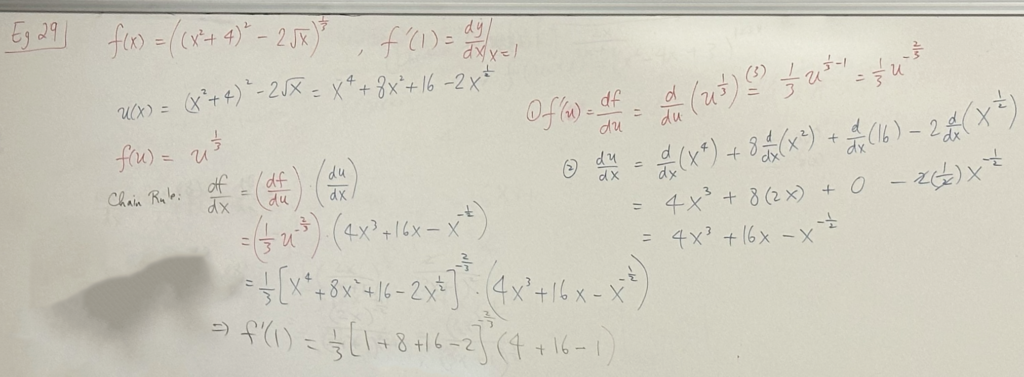
\( y = \sqrt{\frac{2x}{3x+1}}, find \frac{dy}{dx}|_{x=1}. \)

\( u(x) = \frac{2x}{3x+1} \to \frac{du}{dx} = ? \) (1)

\( f(u) = \sqrt{u} \to \frac{df}{du} = ? \) (2)

check \(f(u(x)) = \sqrt{\frac{2x}{3x+1}}\)

(1) \( u(x) = \frac{2x}{3x+1} \to \frac{du}{dx} = ? \)

\( \frac{du}{dx} = \frac{d}{du}(\sqrt{u}) = \frac{d}{du}(u^{\frac{1}{2}) [DR3] = \frac{1}{2}u^{\frac{1}{2}-1} = \frac{1}{2}u^{-\frac{1}{2}} \)

(2) \( f(u) = \sqrt{u} \to \frac{df}{du} = ? \)

\( \frac{du}{dx} = \frac{d}{dx} (\frac{2x}{3x+1}), 2x = a(x), 3x+1 = b(x) [DR7] \)

\( \frac{da}{dx}= \frac{d}{dx}(2x) = 2\)

\( \frac{db}{dx} = \fraac{d}{dx}(3x+1)={d}{dx}(3x)+\frac{d}{dx}(1) = 3 \)

\( = \frac{(\frac{da}{dx}) \times b(x) – (\frac{ab}{ax})a(x)}{[b(x)]^{2}} \)

\( = \frac{(2)(3x+1)-(3)(2x)}{(3x+1)^{2}}\)

\( = \frac{6x+2-6x}{(3x+1)^{2}} = \frac{2}{(3x+1)^{2}} \)

Chain Rule (8): \( \frac{df}{dx} \frac{df}{du} \times \frac{du}{dx} \)

\( = ( \frac{1}{2}u^{-\frac{1}{2}}) \times ( \frac{2}{(3x+1)^{2}}) \)

\( = \frac{1}{2} (\frac{2x}{3x+1})^{-\frac{1}{2}} \cdot \frac{2}{(3x+1)^{2}} \)

\( = \frac{(2x)^{-\frac{1}{2}}}{(3x+1)^{2-\frac{1}{2}}} = \frac{(2x)^{-\frac{1}{2}}}{(3x+1)^{\frac{3}{2}}} \to \frac{df}{dx}|_{x=1} = \frac{dy}{dx}|_{x=1} \)

\( = \frac{(2)^{-\frac{1}{2}}{(3+1)^{3}{2}} = \frac{(2)^{-\frac{1}{2}}{4^{7}{2}} \)

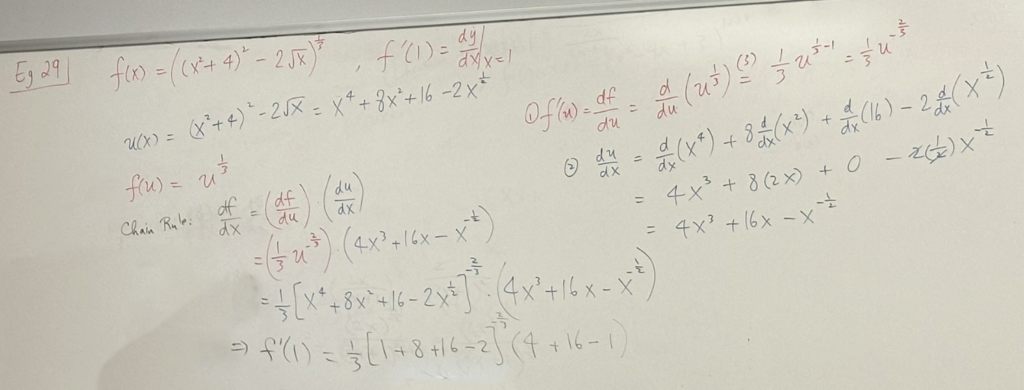
\( f(x) = ( ( x^{2} + 4 ) ^{2} – 2\sqrt{x} )^{\frac{1}{3}}, f'(1) = \frac{dy}{dx}|_{x=1} \)

\( u(x)= (x^2 +4)^2 – 2\sqrt{x} \to \frac{du}{dx} \)

\( f(u) = u^{\frac{1}{3}} \to \frac{df}{du} \)

(1) \( f'(u) = \frac{df}{du} = \frac{d}{du}(u^{\frac{1}{3}}) [DR3] = \frac{1}{3}u^{\frac{1}{3}-1} \frac{1}{3}u^{-\frac{2}{3}} \)

(2). \( \frac{du}{dx} =\frac{d}{dx}(x^4) + 8\frac{d}{dx}(x^2) + \frac{d}{dx}(16) + 2\frac{d}{dx}(x^{\frac{1}{2}}) \)

\( =4x^3 +8(2x) +0 – 2(\frac{1}{2}) x^{-\frac{1}{2}} \)

\( = 4x^3 + 16x – x^{-\frac{1}{2}} \)

Chain Rule: \( \frac{df}{du} \cdot \frac

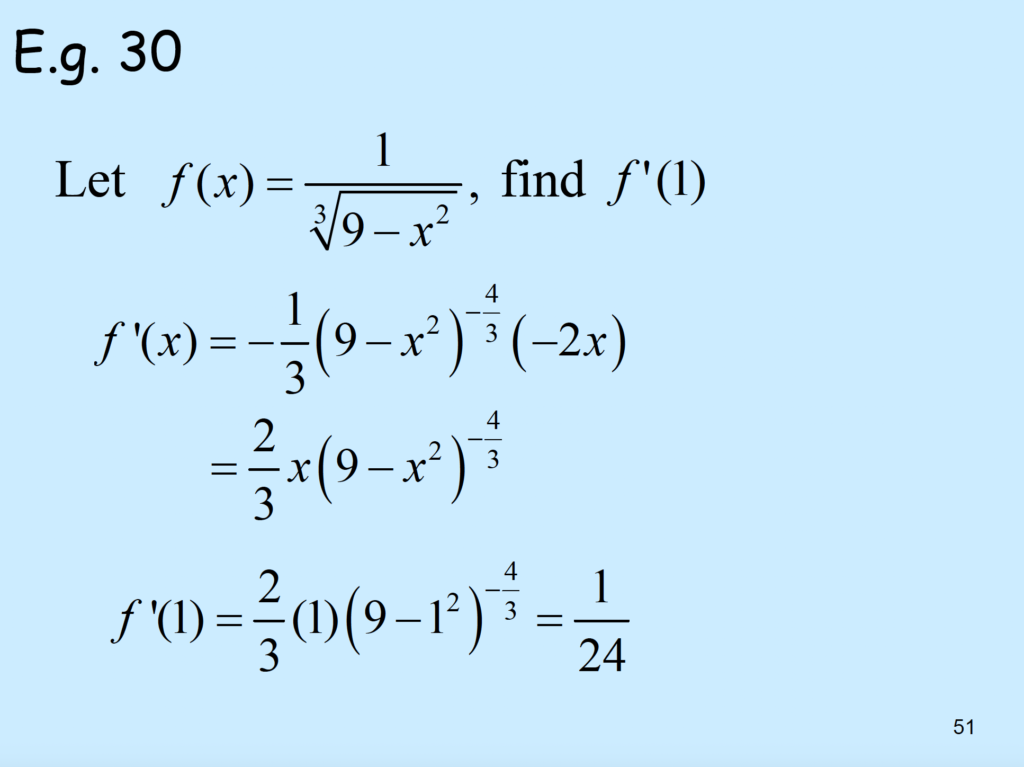
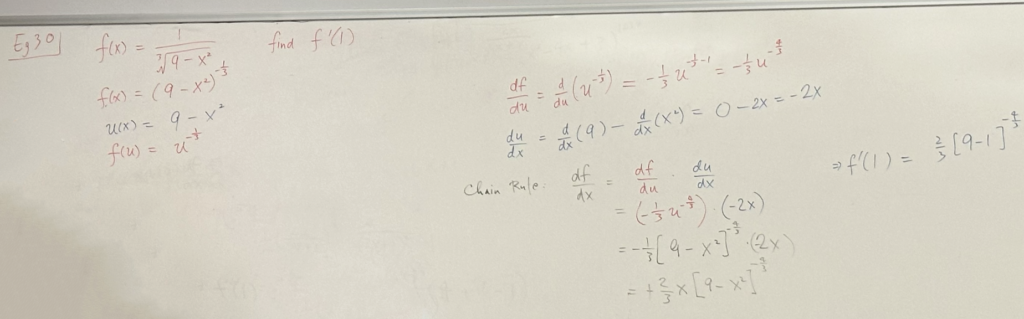
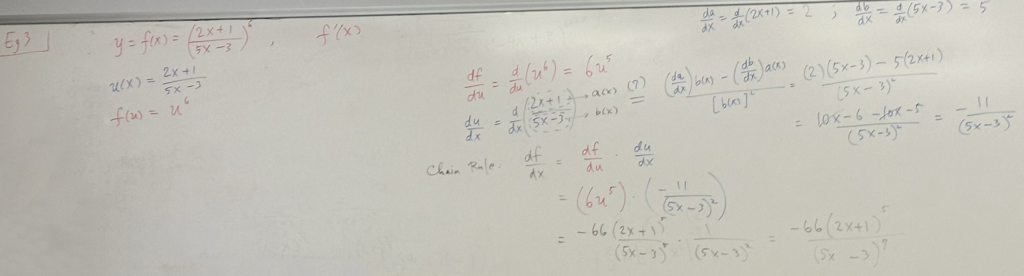
Second derivative

\( \frac{d^2}{dx^2} \neq (\frac{dy}{dx})^2 \)

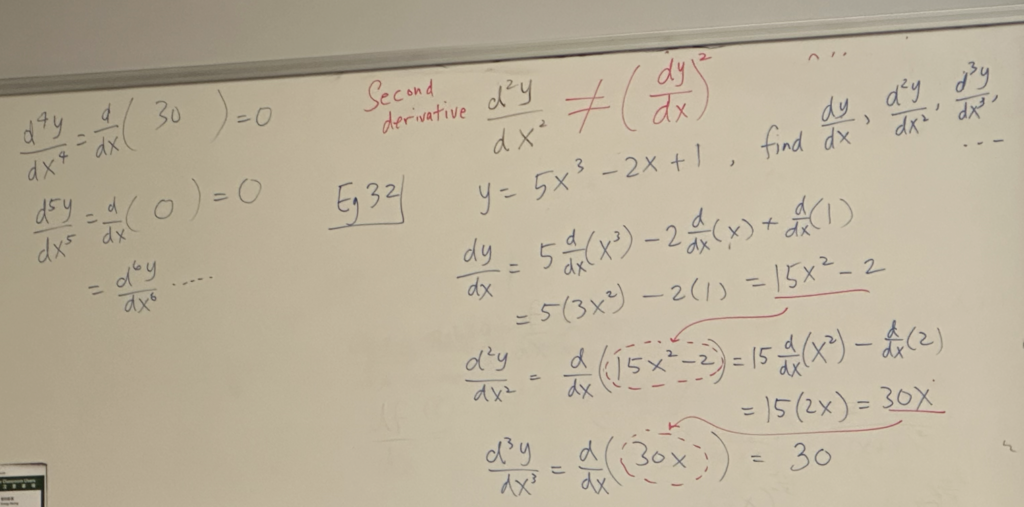
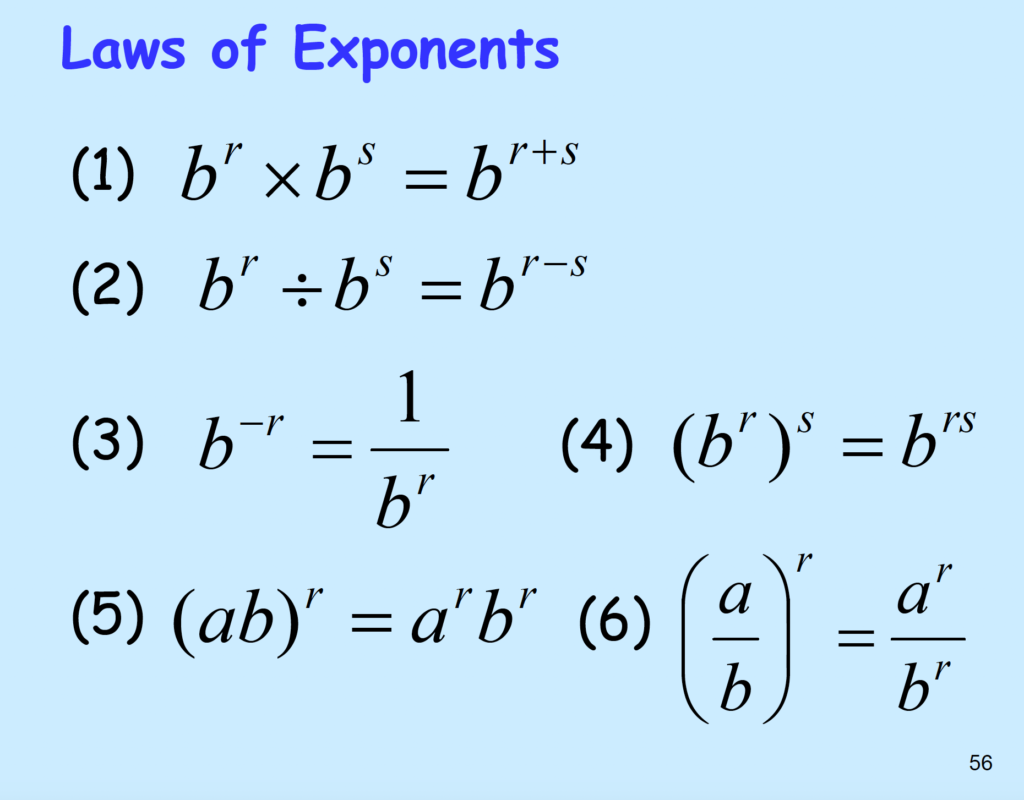
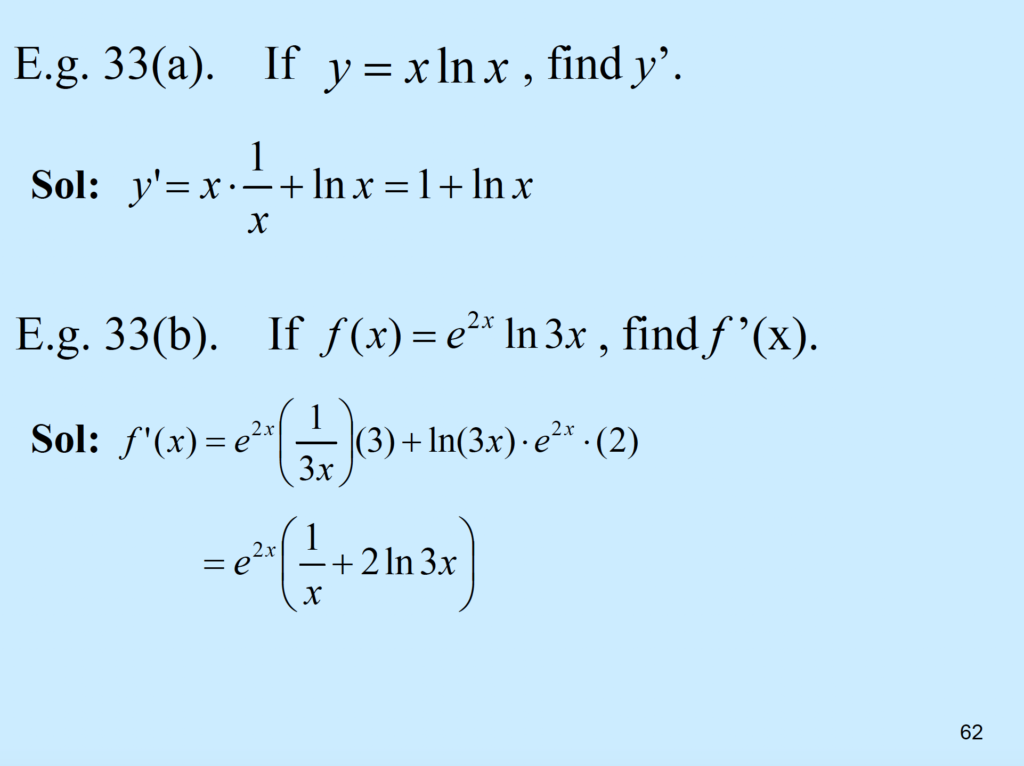
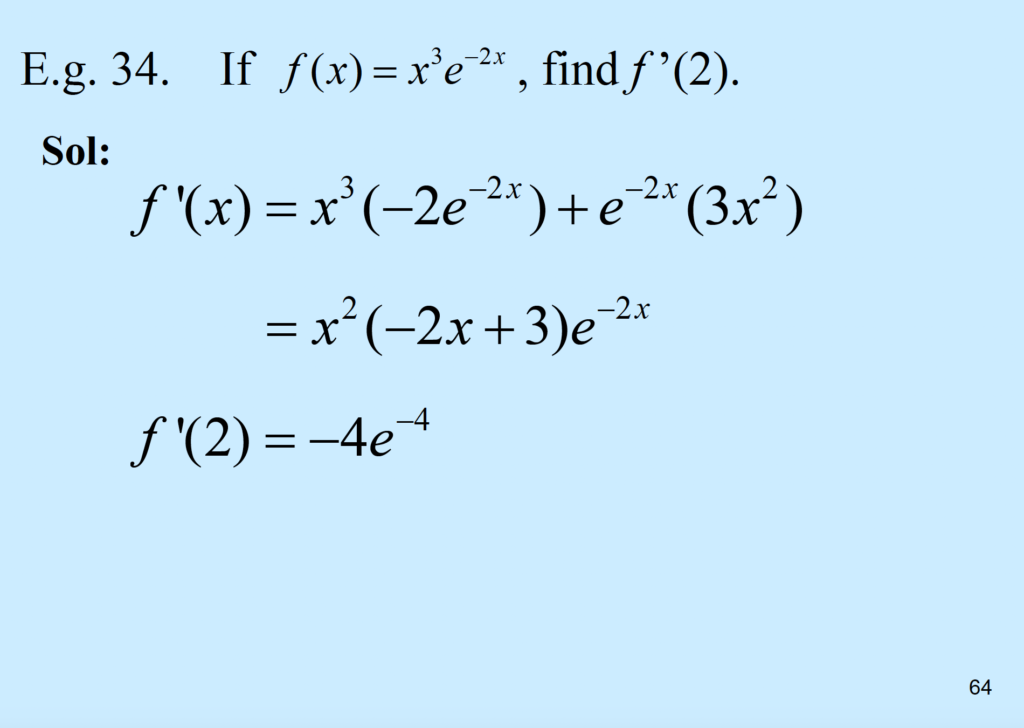
\( f(x) = x^{3}e^{-2x}\), find \( f'(2) = \frac{df}{dx}|_{x=2} \)

Product Rule \( \frac{df}{dx} = \frac{d}{dx}(x^3 \times e^{-2x})\)

\( = \frac{d}{dx}(x^3) \times e^{-2x} + \frac{d}{dx}(e^{-2x}) \times x^3\)

(1) \( \frac{d}{dx}(x^3) = 3x^2\)

(2) \( \frac{d}{dx}(e^{-2x})[DR11] = e^{-2x}(-2) \)

\( \to u(x) = -2x, \frac{du}{dx} = -2 \)

\( =(3x^2) \times e^{-2x} + (-2e^{-2x}) \times x^3 \)

\( = e^{-2x}x^2(3-2x) \)

\( f'(2) = e^{-2(2)} (2)^2 (3-2(2)) \)

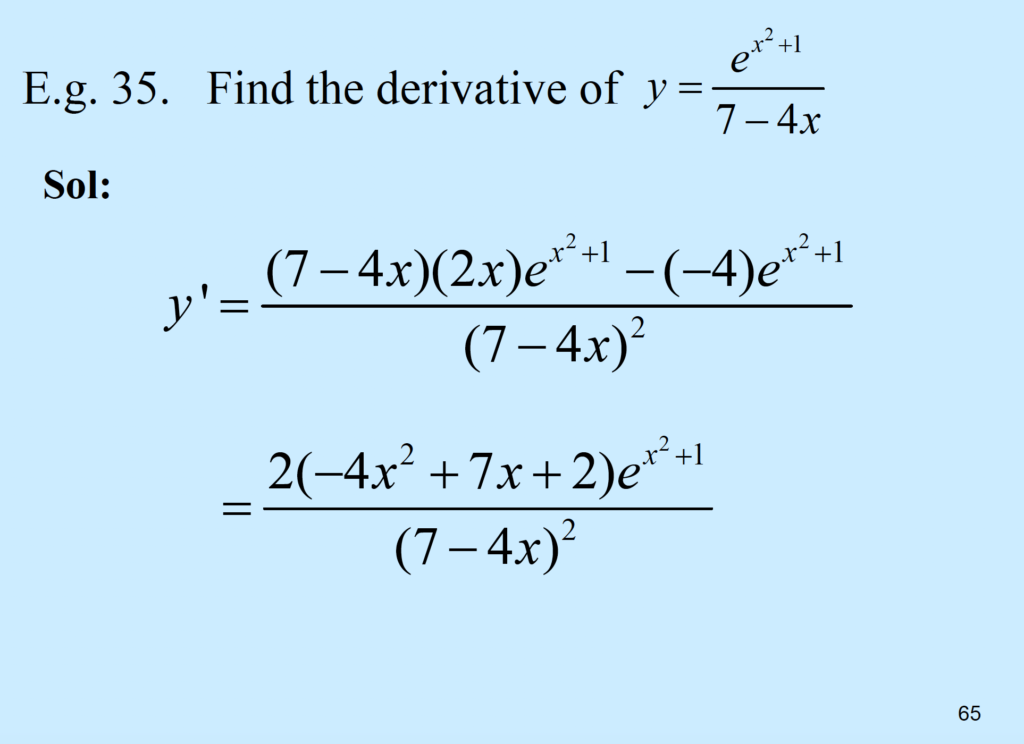
Find the derivative of \( y=\frac{e^{x^2+1}}{7-4x} \).

By quotient rule [DR7],

\( \frac{dy}{dx} = \frac{\frac{d}{dx}(e^{x^2+1}) \times (7-4x) – \frac{d}{dx}(7-4x) \times e^{x^2+1}}{(7-4x)^2} \)

(1) \( \frac{d}{dx}(e^{x^2+1}) = e^{x^2+1} \times (2x) \)

\( u(x) = 2xe^{x^2+1} \)

(2) \( \frac{d}{dx}(7-4x) = -4\)

\( = \frac{(2xe^{x^2+1} \times (7-4x) -(-4) \times e^{x^2+1}}{(7-4x^2)} \)

\( = \frac{e^{x^2+1}[14x-8x^2+4]}{(7-4x)^2} \)

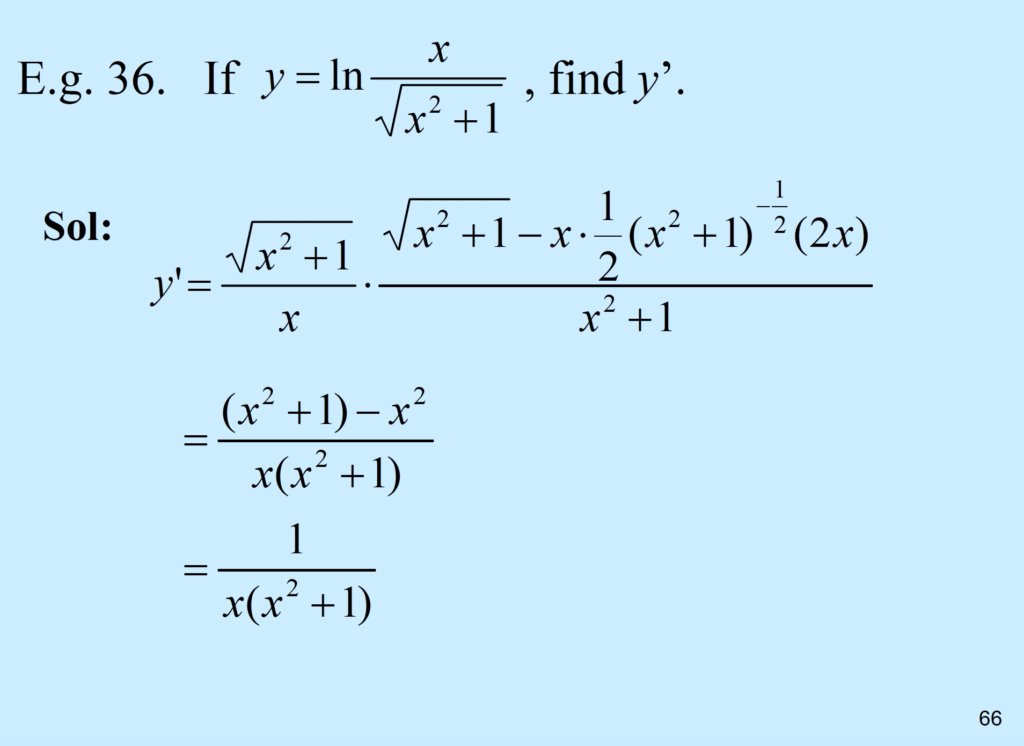
\( y = ln(\frac{x}{\sqrt{x^2+1}}) \)

The fraction is inside \( ln\), so that we (do something) to simply the equation of y. (refer to the properties of \( log\))

\( = ln(x) – ln(\sqrt{x^2+1}) \)

\( = ln(x) -ln( (x^2+1)^{\frac{1}{2}} \)

\( = ln(x) – \frac{1}{2}ln(x^2+1) \)

\( \to y = ln(x) – \frac{1}{2}ln(x^2+1) \)

\( \frac{dy}{dx} = \frac{d}{dx} ln(x) – \frac{1}{2} \frac{d}{dx} ln(x^2+1) \)

\( = \frac{1}{x} – \frac{1}{2}\frac{1}{x^2+1} \times (2x) \)

\( u(x) = x^2+1 \)

\( \frac{du}{dx} = \frac{d}{dx}(x^2+1) = 2x \)

\( = \frac{1}{x} – \frac{x}{(x^2+1)} \)

\( = \frac{(x^2+1)-x^2}{x(x^2+1)} = \frac{1}{x(x^2+1)} \)

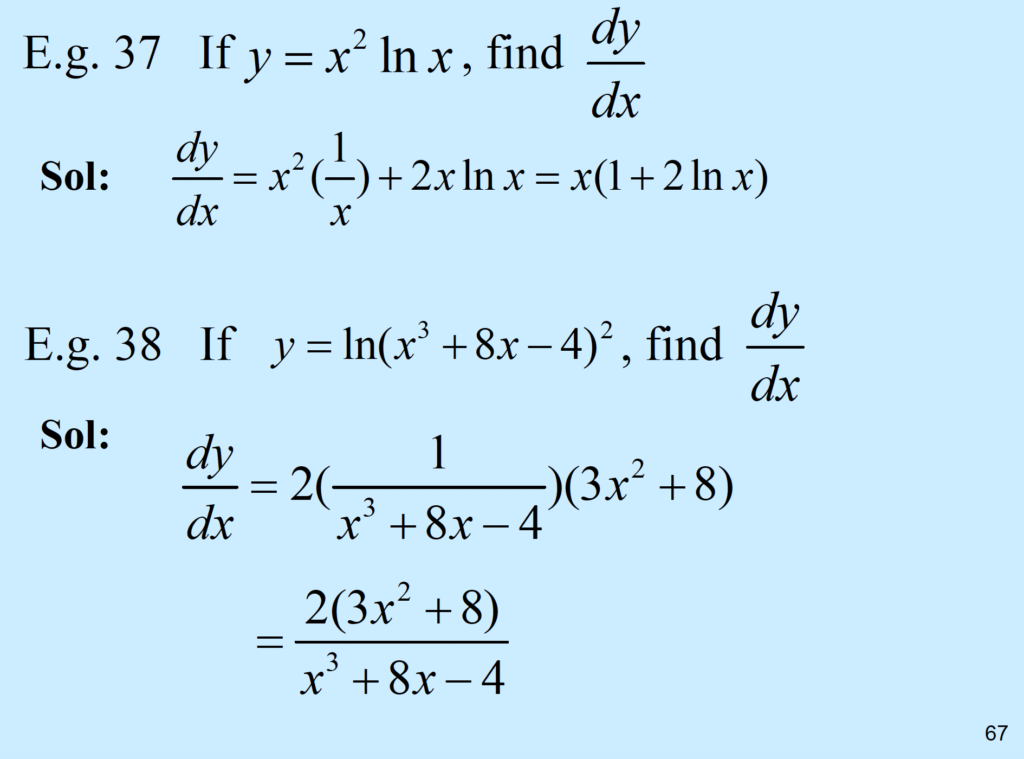
Eg 39

\( y = (x^2)(ln x), find \frac{dy}{dx} \)

Product rule \( \frac{dy}{dx} = \frac{d}{dx}(x^2) \times ln x + \frac{d}{dx}(ln x) \times x^2 \)

\( = 2x \times ln x+ (\frac{1}{x}) \times x^2\)

\( = 2x ln x + x \)

Eg 40

\( y = ln (x^3 + 8x -4 )^2, find \frac{dy}{dx} \)

Using \( ln \) property4,

\( \to \frac{dy}{dx} = 2 ln( x^3 +8x-4) \)

\( u(x) = x^3+8x-4 \)

\( \frac{du}{dx} = 3x^2+8 \)

[DR12], \( = 2 \frac{1}{(x^3+8x-4)} \times (3x^2 + 8) \)

\( = \frac{2(3x^2+8)}{(x^3+8x-4)} \)

Stationary point (s) \( (X_{0}) \)

\( y= f(x), \frac{dy}{dx}|_{x=x_0} = 0 , y_0 = f(x_0) \)

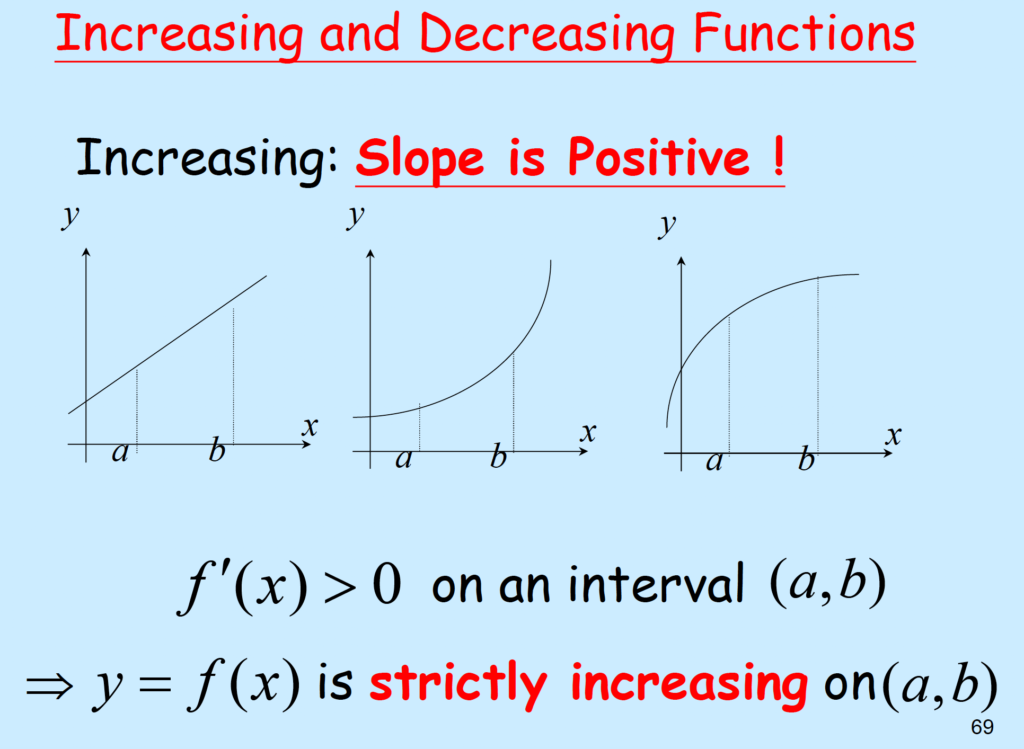
\( Slope_{at pt x} f'(x) , if f'(x) >0\), f is increasing at x. if f'(x) <0, f is decreasing at x. \)

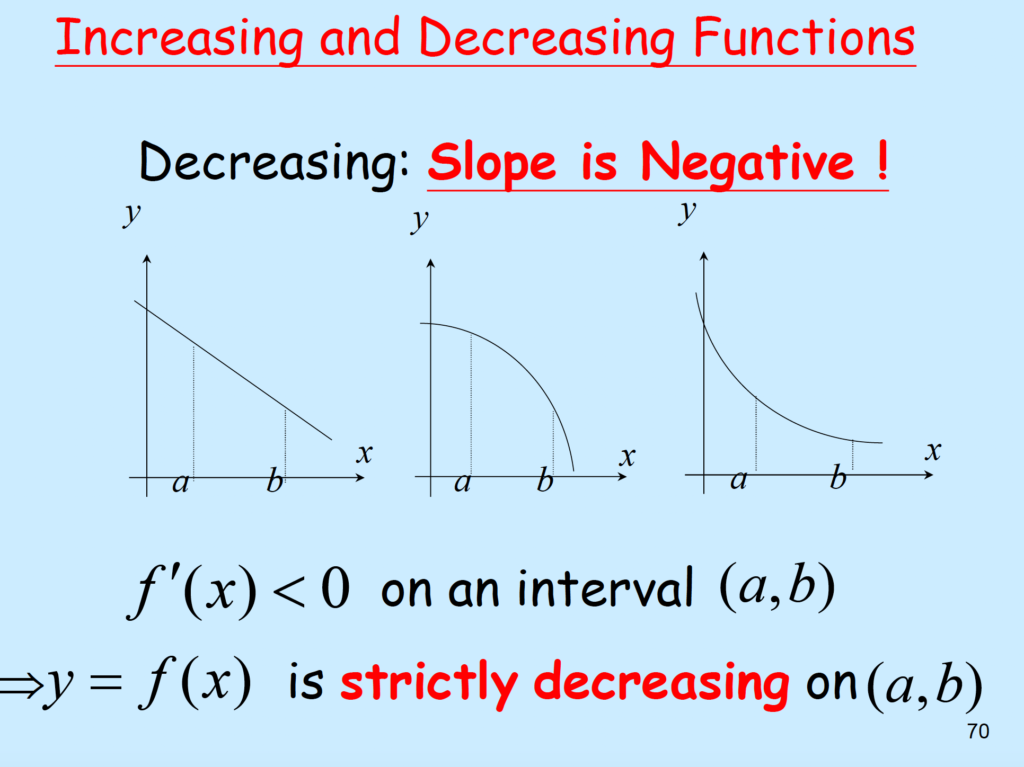
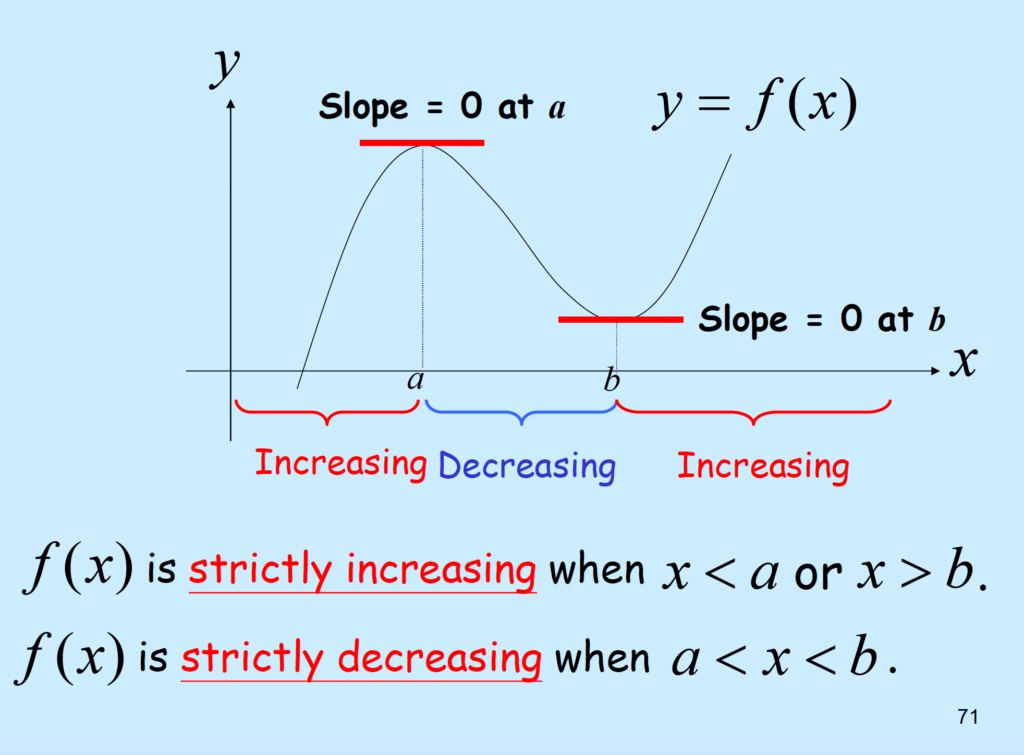
Stationary points (s) are denoted as (a, f(a)) and (b, f(b)).

First Derivative Test

1. Find all stationary pts. i.e. find \(x_0\) such that \(f'(x_0) = 0\)
2. 
   (x0,y0) is min
   (x0,y) is max
   Otherwise, (x0,y0) is neither max/min.

---

Eg 39

1. Find all stationary pts, i.e. find x0 such that f'(x0) = 0 .
   \( \frac{df}{dx} = 2x = 0 \to x = 0, y= f(0) = 0^2 = 0 \to (0,0) \)is stationary pt.
2. 1. \(f'(x)\) for \(x<0 \) = 2x < 0; Example: x=-1, –> f'(-1) = -2 <0
   2. \( f'(x), \) for x>0 =2x > 0; Example, x=1 –> f'(1) =2>0
   
3. \( \to y=x^2 \) has a min. point at (0,0)

---

Eg 40

1. \(f'(x) = -2x =0 \to x_0 = 0\)
   \(y_0 = f(x_0) = -(0)^2 = 0\)
   \((x_0,y_0) = (0,0)\) is stationary pt.
2. 1. \(f'(x) = -2x > 0, when x<0 \)\(f'(x) = -2x <0, when x > 0 \)
   
3. \( (0,0) \) is the max!

---

Eg 41

1. \( y=f(x)=2x^2-\frac{2}{3}x^3 \)
2. Find all stationary pts, i.e. find \(x_0\) such that \( f'(x) = 4x-2x^2 = 0 = 2x(2-x) =0\)
3. \( \to x=2\) or \( x=0\)
4. 1. When x=0, \(f(0) = 2(0)^2 – \frac{2}{3}(0)^3 = 0 \to (0,0) \)When x=2, \(f(2) = 2(2)^2 – \frac{2}{3}(2)^3 = \frac{8}{3} \to (2,\frac{8}{3}) \)

x	x<0	x=0	0<x<2	x=2	x>2
f'(x)	-ve	0	+ve	0 (By def., s.p. itself =0)	-ve
f(x)	–	min	+	max	–

\(f'(x) = 2x(2-x) \to f'(x) <0\) when \(x <0\).

\(f'(x) = 2x(2-x) \to f'(x) >0\) when \(0<x<2\).

\(f'(x) = 2x(2-x) \to f'(x) <0\) when \(x >2\).

\( \to (0,0)\) is min

\( (2,\frac{8}{3})\) is max

---

Eg42

\( y=f(x) = x^3 -3x+2 \)

1. Find all stationary pt(s), i.e. find \(x_0\) such that \(f'(x_0) = 0 \)
   
   \( f'(x) = 3x^2 -6x=0\)
   \(3x(x-2)=0 \to x=0 \) or \(x=2\)
2. When \(x=0\), \(f(0) = (0)^3 – 3(0)^2 +2=2 \to (0,2)\)
3. When \(x=2\), \( f(2) = (2)^3 – 3(2)^2 +2 = -2 \to (2,-2) \)
4. (0,2) and (2,-2) are stationary pt(s).

x	x<0	x=0	0<x<2	x=2	x>2
f'(x)	+ve	0	-ve	0	+ve
f(x)	+	max	–	min	+

\( f'(x) = 3x(x-2) \to \)

\( f'(x) > 0 \) when \( x<0\)

\( f'(x) <0\) when \( 0<x<2 \)

\( f'(x) >0\) when \(x>2\)

\( \to (0,2) is max\); \( (2,-2)\) is min.

---

Concavity

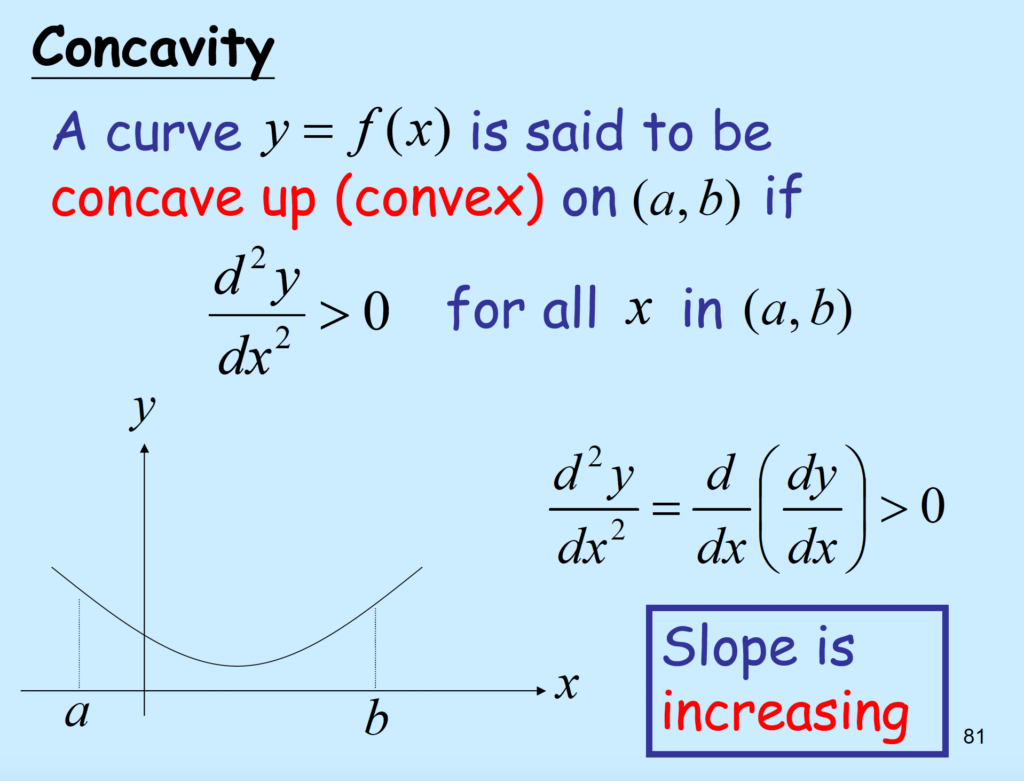
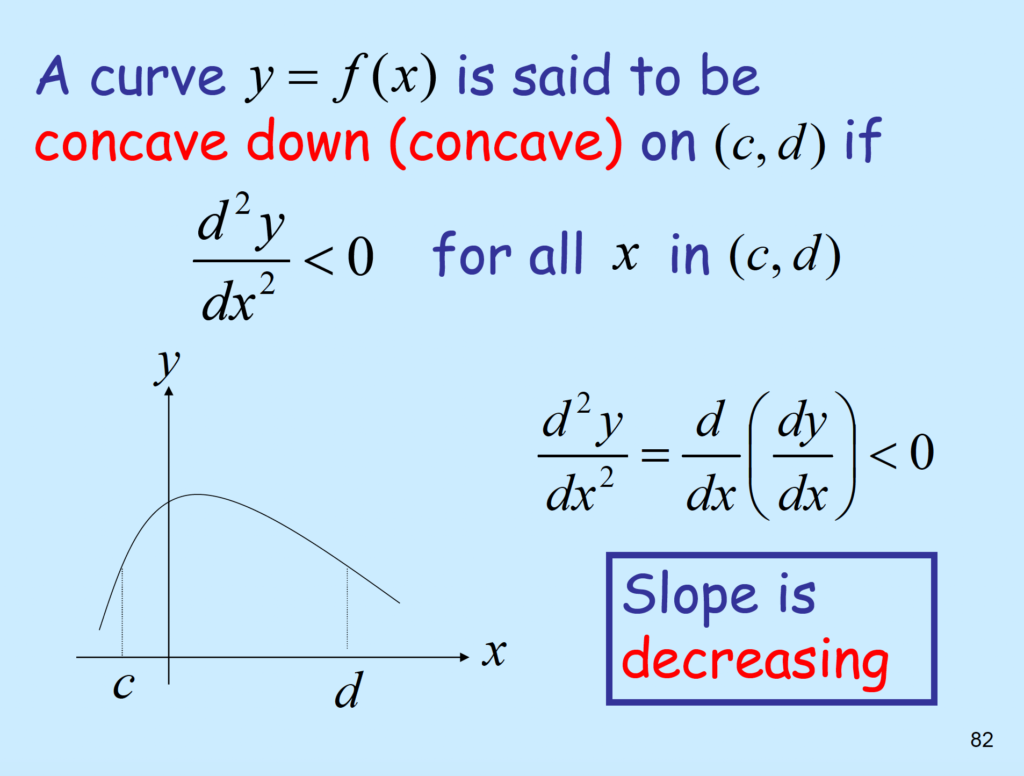
\( y= f(x) \)

1. \( \frac{d^{2}y}{dx^2} = f”'(x) = \frac{d}{dx}(f”(x)) >0 \to \) Concave up.
2. \( \frac{d^{2}y}{dx^2} < 0 \to \) Concave down.

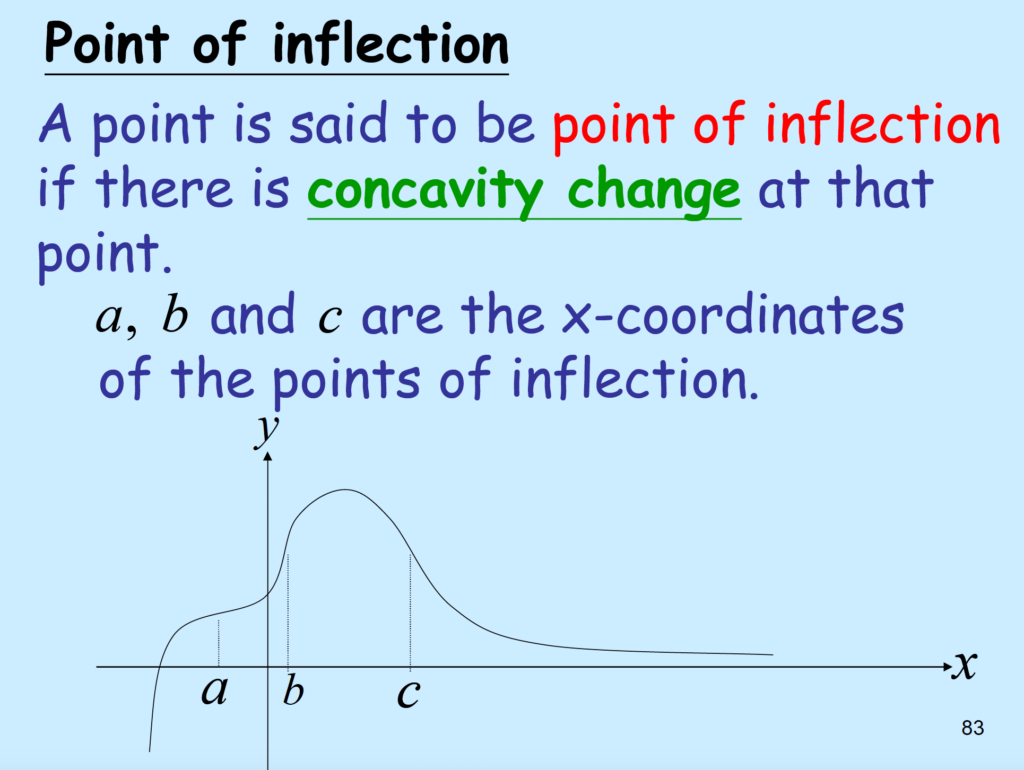
\( \to \frac{d^{2}f}{dx^2}|_{x=a} = 0\)

\( \to \frac{d^{2}f}{dx^2}|_{x=b} = 0\)

\( \to \frac{d^{2}f}{dx^2}|_{x=c} = 0\)

These are the inflection points. \( \frac{d^{2}f}{dx^2} \)

Differ from stationary points, which denoted by \( (\frac{df}{dx} = 0 )\)

---

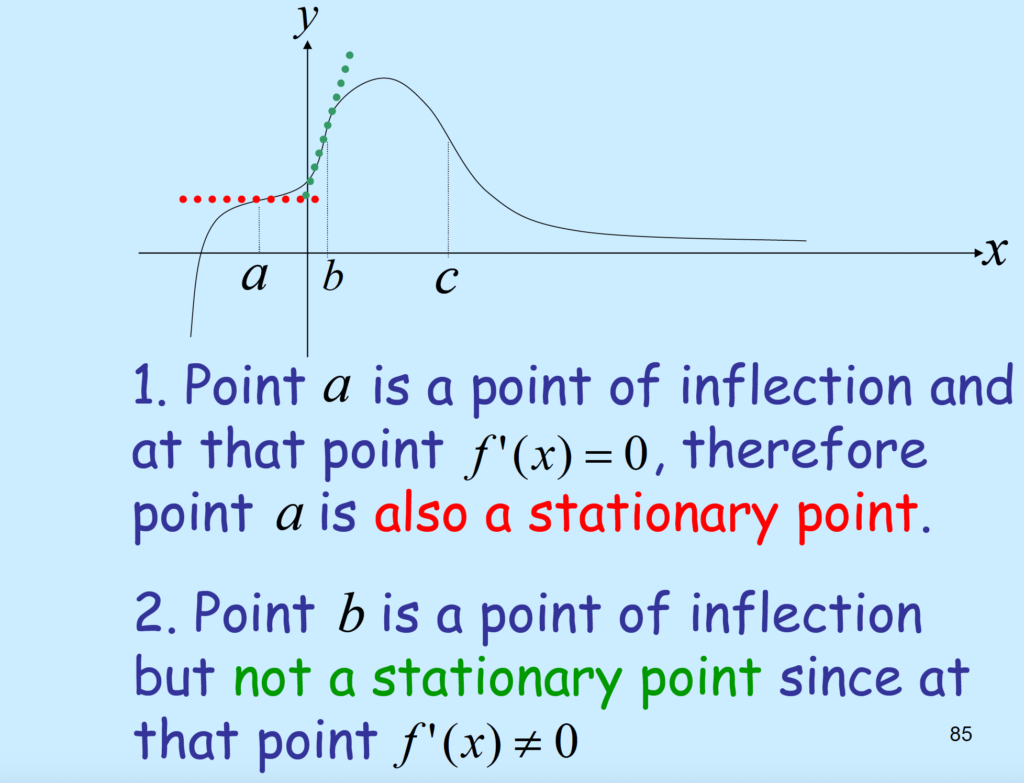
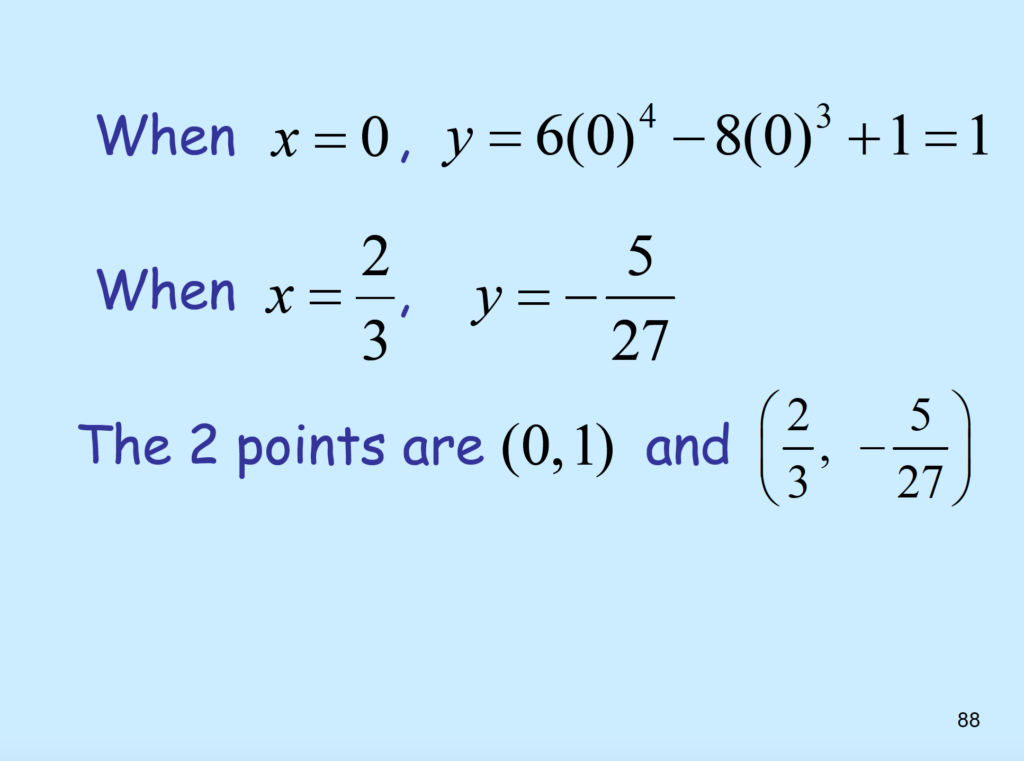
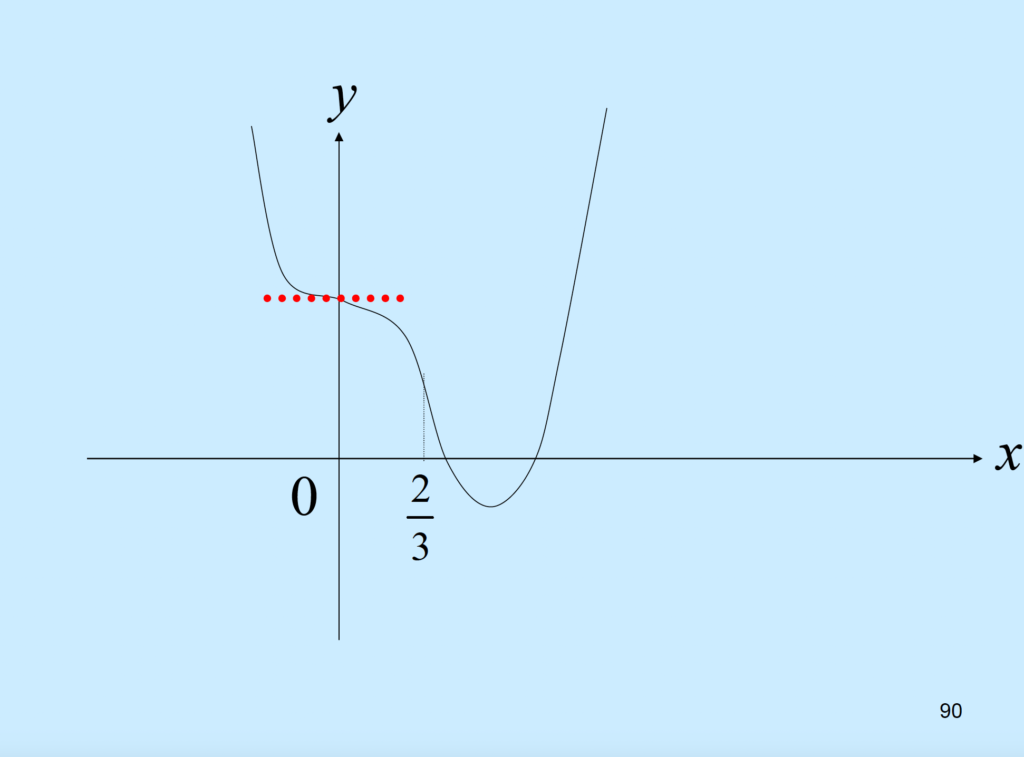
Eg 43

\( y =f(x) = 6x^4 – 8x^3 +1 \)

1. Find out all inflection pts, i.e., find all x such that \( \frac{d^{2}f}{dx^2} = 0 \).

\( f'(x) = 24x^3 – 24x^2 \)

\( f'(x) = 72x^2 – 48x =0 \)

\( 12x(6x-4) = 0\)

\( \to x = 0 \) or \( x = \frac{2}{3} \)

\( \to f(0) =1 \)

(0,1)

\( \to \frac{2}{3} \)

\(= -\frac{5}{27} \)

\(( \frac{2}{3}, \frac{-5}{27} )\)

are inflection pts.

Test for concavity:

x	x<0	x=0	0<x<\( \frac{2}{3}\)	x=\( \frac{2}{3}\)	x>\( \frac{2}{3}\)
f”(x)	+ve	0	-ve	0	+ve
f(x)	Concave up	Inflection pt	Concave down	Inflection pt	Concave up

1. \( f”(x) >0\) when \(x <0 \)
2. \( f”(x) <0\) when \(0<x<\frac{2}{3} \)
3. \( f”(x) >0\) when \(x>\frac{2}{3} \)

\( f”(x) = 24x(3x-2) \)

Wrote at 2023-10-10.

Ch2 eX, ex8-10

2023-10-17 4:56:00

Eg44 \( y= 12x-3x^2 -2x^3\), find inflection pts.

\( y’=12-6x-6x^2\)

\(y”=-6x-12x=0\)

\(-6(1+2x)=0 \to x=-\frac{1}{2}\)

When \(x=-\frac{1}{2},xxx\)