

Such a mathematical process of deducing the general result is called induction. However, the validity of the above identity is questionable since it has not been tested for all positive integers. To resolve such a difficulty, a mathematical procedure known as Mathematical Induction (M.I.) is introduced.
Example

1. Base Step: Show P(1) is true
P(n): 1+3+5+7+ … + (2n-1) = \(n^{2}\)
P(1): LHS: 2(1)-1 =1
RHS: \((1)^{2}\) = 1
LHS=RHS for P(1)
2. Inductive Step: Assume P(k) is true.
P(k) = 1+3+5+7+…+(2k-1) = \(k^{2}\)
We need to show P(k+1) is true, i.e.: LHS = RHS for P(k+1)
Let’s see.
P(k+1) LHS: 1+3+5+7+…+(2K-1) + (2(k+1)-1)
RHS: \((k+1)^{2}\)
We are going to show LHS= RHS
LHS: 1+3+5+7+….+(2k-1)+(2(k+1)-1)
= \(k^{2}\) +(2(k+1)-1)
= \(k^{2}\) +2k+2-1
= \(k^{2}\) +2k+1
= \((k+1)^{2}\) = RHS
By M.I., P(n) is true for all n \(\geq\) 1


1. Basic step: Show P(1) is true
P(n): 1×2 + 2×3 + \(2^{2}\)x4 + …+ \(2^{n-1}\)(n+1) = \(2^{n}\)(n)
When n=1,
LHS: \(2^{1-1}\)(1+1) = \(2^{0}\)(2) = 2
RHS: \(2^{1}\)(1) =2
LHS=RHS for P(1).
2. Inductive step: Assume P(k) is true
P(k) = 1×2 + 2×3 + \(2^{2}\) x4 + … + \(2^{k-1}\)(k+1) = \(2^{k}\)(k)
We need to show P(k+1) is true.
Let’s prove.
P(k+1):
LHS = 1×2 + 2×3 + \(2^{2}\)x4 + … + \(2^{k-1}\)(k+1) + \(2^{(k+1)-1}\)((k+1) +1)
RHS = \(2^{(k+1)}\)(k+1)
By assumption, 1×2 + 2×3 + \(2^{2}\)x4 + … + \(2^{k-1}\)(k+1) = \(2^{k}\)(k)
1×2 + 2×3 + \(2^{2}\)x4 + … + \(2^{k-1}\)(k+1) + \(2^{(k+1)-1}\)((k+1) +1)
= \(2^{k}\)(k) + \(2^{(k+1)-1}\)((k+1) +1)
= \(2^{k}\) (k) + \(2^{k}\)(k+2)
= \(2^{k}\)(k+k+2)
= \(2^{k}\)(2k+2)
= \(2^{k}\)2{k+1}
=\(2^{k+1}\)(k+1)
=RHS
Start with Base k then inductive step.

Idea behind Inductive step: Assume P(k) is true, prove (k+1) step.
Exercise:
Q17
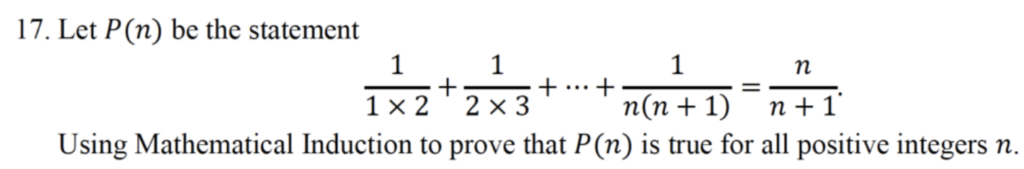
1. Basic step: Show P(1) is true.
P(n) = \(\frac{1}{1×2} + \frac{1}{2×3} + … + \frac{1}{n(n+1)} = \frac{n}{n+1}\)
When n=1,
LHS: \(\frac{1}{1×2} + \frac{1}{2×3} + … + \frac{1}{1(1+1)} = \frac{1}{1+1}\)
= \(\frac{1}{2}\)
= RHS = \(\frac{1}{2}\)
2. Inductive step: Assume P(k) is true
P(k) = \(\frac{1}{1×2} + \frac{1}{2×3} + … + \frac{1}{k(k+1)} = \frac{k}{k+1}\)
We need to show P(k+1) is true.
Let’s prove
P(k+1):
RHS = \( \frac{(k+1)}{(k+1)+1} \)
= \( \frac{(k+1)}{(k+2)} \)
LHS = \(\frac{1}{1×2} + \frac{1}{2×3} + … + \frac{1}{k(k+1)} + \frac{1}{(k+1)(k+1+1)} \)
= \( \frac{k}{k+1} + \frac{1}{(k+1)(k+1+1)} \)
= \( \frac{k(k+1+1)+1}{(𝑘+1)(𝑘+1+1)} \)
= \( \frac{k(k+2)+1}{(k+1)(k+2)} \)
= \( \frac{k^{2}+2k+1}{(k+1)(k+2)} \)
= \( \frac{(k+1)^{2}}{(k+1)(k+2)} \)
= \( \frac{(k+1)}{(k+2)} \)
= RHS
Q18
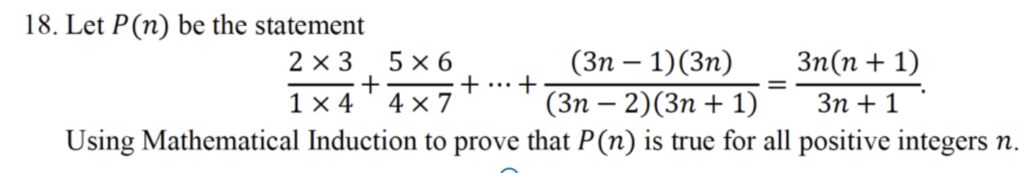
1. Basic Step: Show P(1) is true.
\( P(n) = \frac{2×3}{1×4} + \frac{5×6}{4×7} + … + \frac{(3n-1)(3n)}{(3n-2)(3n+1)} = \frac{3n(n+1)}{3n+1} \)
When n=1,
LHS: \( \frac{2×3}{1×4} + \frac{5×6}{4×7} + … + \frac{(3(1)-1)(3(1))}{(3(1)-2)(3(1)+1)} \)


